Решение и ответы заданий Варианта №2 из сборника ЕГЭ 2024 по математике (профильный уровень) под редакцией И.В. Ященко 36 вариантов ФИПИ. ГДЗ профиль для 11 класса. Полный разбор.
Задания №14,17,18,19 долго оформлять, решу их позже, если будет время и желание. Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
В треугольнике ABC угол C равен 90°, BC = 3, cosA = \frac{2\sqrt{5}}{5}. Найдите AC.
Задание 2.
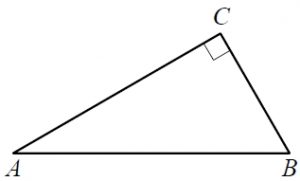
На координатной плоскости изображены векторы \overrightarrow{a} и \overrightarrow{b}. Найдите скалярное произведение векторов 2\overrightarrow{a} и \overrightarrow{b}.
Задание 3.
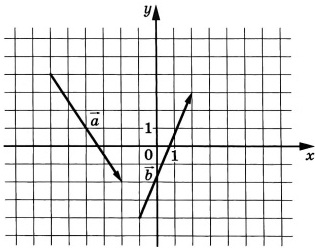
В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,6 раза. Найдите объём детали. Ответ выразите в куб. см.
Задание 4.
На конференцию приехали учёные из трёх стран: 8 из Уругвая, 7 из Чили и 5 из Парагвая. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что вторым окажется доклад учёного из Чили.
Задание 5.
На одной полке стоит 25 блюдец: 16 красных и 9 синих. На другой полке стоит 25 чашек: 13 красных и 12 синих. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Задание 6.
Найдите корень уравнения 2^{log_{16}(5x+4)}=5.
Задание 7.
Найдите значение выражения (1257)3:(254)8.
Задание 8.
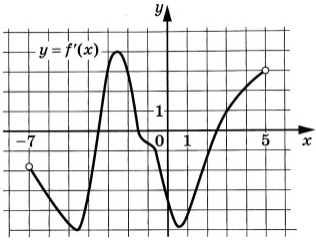
На рисунке изображен график y = f‘(x) – производной функции f(x), определенной на интервале (–7;5). Найдите промежутки убывания функции f(x). В ответ укажите сумму целых точек, входящих в эти промежутки.
Задание 9.
В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону H(t) = H0 − \sqrt{2gH_{0}}kt + \frac{g}{2}k2t2, где t – время в секундах, прошедшее с момента открытия крана, H0 = 20 м – начальная высота столба воды, k = \frac{1}{200} – отношение площадей поперечных сечений крана и бака, а q – ускорение свободного падения (считайте q = 10 м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?
Задание 10.
Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 120 литров она заполняет на 2 минут быстрее, чем первая труба?
Задание 11.
На рисунке изображен график линейной функции. Найдите значение x, при котором f(x) = 8.
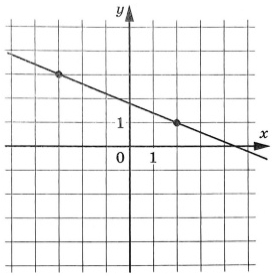
Задание 12.
Найдите точку максимума функции y = (x − 14)2∙e26−x.
Задание 13.
а) Решите уравнение cosx·cos2x – sin2x – cosx = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку [-\frac{5\pi}{2};-\pi].
Задание 14.
В основании прямой призмы ABCDAlB1C1D1 лежит параллелограмм ABCD. На рёбрах А1В1, В1С1 и ВС отмечены точки М, К и N соответственно, причём В1К:КС1 = 2:3. Четырёхугольник AMKN – равнобедренная трапеция с основаниями 4 и 5.
а) Докажите, что точка N – середина ребра ВС.
б) Найдите площадь трапеции AMKN, если объём призмы равен 20, а высота призмы равна 2.
Задание 15.
Решите неравенство 3^{2\sqrt{x}-10}+6561\cdot 12^{\sqrt{x}-4}<3^{2\sqrt{x}}+16\cdot 12^{\sqrt{x}-6}.
Задание 16.
В июле 2026 года планируется взять кредит на десять лет в размере 1300 тыс. рублей. Условия возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
– в июле 2027, 2028, 2029, 2030 и 2031 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
– в июле 2032, 2033, 2034, 2035 и 2036 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2036 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 2780 тыс. рублей. Сколько рублей составит платёж в 2027 году?
Задание 17.
Прямая, перпендикулярная стороне AB ромба ABCD, пересекает его диагональ АС в точке K, а диагональ BD в точке L, причём AK:KС = 1:3, BL:LD = 2:1.
а) Докажите, что прямая KL делит сторону ромба AB в отношении 1:4.
б) Найдите сторону ромба, если KL = 6.
Задание 18.
Найдите все значения а, при каждом из которых система уравнений
\begin{cases} (xy–4x+20)\cdot \sqrt{y–4x+20}=0, \\ y=5x+a \end{cases}
имеет ровно два различных решения.
Задание 19.
В классе больше 10, но не больше 27 учащихся, а доля девочек не превышает 26%.
а) Может ли в этом классе быть 6 девочек?
б) Может ли доля девочек составить 30%, если в этот класс придёт новая девочка?
в) В этот класс пришла новая девочка. Доля девочек в классе составила целое число процентов. Какое наибольшее число процентов может составить доля девочек в классе?
Источник варианта: Сборник ЕГЭ 2024. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.