Решение и ответы заданий № 1–12 варианта №336 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
Найдите двузначное число, если известно, что цифра его единиц на 2 больше цифры десятков и что произведение искомого числа на сумму его цифр равно 144.
Задание 2.
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указываются дата и время суток, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку, на сколько градусов Цельсия наибольшая температура 13 мая превышала наибольшую температуру 11 мая?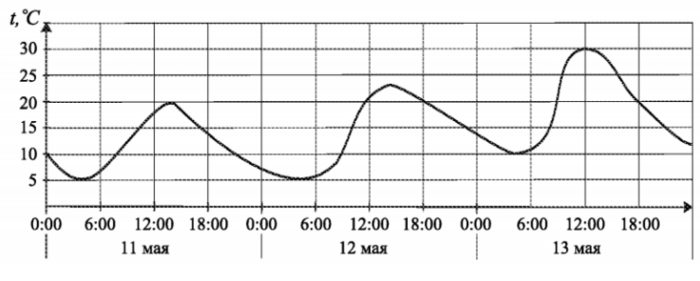
Задание 3.
Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (cм. рис.). Ответ дайте в квадратных сантиметрах.
Задание 4.
В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% ‐ с заболеванием L, 20% ‐ с заболеванием М. Вероятность полного излечения болезни К равна 0,7; для болезней L и М эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что этот больной страдал заболеванием К. Ответ округлите до сотых.
Задание 5.
Решите уравнение:
Задание 6.
Сторона правильного шестиугольника ABCDEF равна 2020√3. Найдите радиус окружности, вписанной в треугольник MPK, если точки М, Р и К – середины сторон АВ, CD, EF соответственно.
Задание 7.
Прямая y = x + 3 является касательной к графику функции y = ax2 + 3x + c, пересекающему ось ординат в точке А (0; –2). Найдите a.
Задание 8.
Основанием прямой призмы ABCDA1B1C1D1 является прямоугольник ABCD, стороны которого равны 6√5 и 12√5. Высота призмы равна 8. Секущая плоскость проходит через вершину D1 и середины рёбер AD и CD. Найдите косинус угла между плоскостью основания и плоскостью сечения.
Задание 9.
Упростите выражение:
Задание 10.
Сосулька упала с крыши с высоты 40м. Высота h(t), на которой находится падающая сосулька, зависит от времени падения t(c) следующим образом: h(t) = 10 – 5t2. Определите, сколько секунд сосулька будет находиться на высоте не менее 15,8 м.
Задание 11.
Объемы ежегодной добычи нефти первой, второй и третьей скважин относятся как 6:7:10. Планируется уменьшить годовую добычу нефти из первой скважины на 10% и из второй – тоже на 10%. На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился?
Задание 12.
Найдите наибольшее значение функции на отрезке [–2; –1]
Источник варианта: alexlarin.net