Решение №1173 Основанием прямой призмы ABCDA1B1C1D1 является прямоугольник ABCD, стороны которого равны 6√5 и 12√5. C1D1 является прямоугольник ABCD, стороны которого равны 6√5 и 12√5.

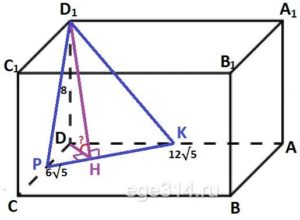
Основанием прямой призмы ABCDA₁B₁C₁D₁ является прямоугольник ABCD, стороны которого равны 6√5 и 12√5. Высота призмы равна 8. Секущая плоскость проходит через вершину D₁ и середины рёбер AD и CD. Найдите косинус угла между плоскостью основания и плоскостью сечения.

Источник: alexlarin.net

Решение:

В сечении получаем ΔPD₁K.
Опустили перпендикуляр D₁H на прямую PK. Т.к. D₁D⊥DH, то DH⊥PK по теореме о трёх перпендикулярах. Необходимо найти cos∠DHD₁
Рассмотрим ΔPDK, он прямоугольный, точки P и K середины сторон призмы, найдём стороны треугольника:

DP = DC/2 = 6√5/2 = 3√5
DK = DA/2 = 12√5/2 = 6√5

Гипотенузу PK найдём по теореме Пифагора:

$PK=\sqrt{(3\sqrt{5})^{2}+(6\sqrt{5})^{2}}=\sqrt{9\cdot 5+36\cdot 5}=\sqrt{225}=15$

Площадь прямоугольного треугольника, это половина произведения катетов:

$S_{\Delta }=\frac{1}{2}\cdot DP\cdot DK=\frac{1}{2}\cdot 3\sqrt{5}\cdot 6\sqrt{5}=9\cdot 5=45$

Площадь этого же треугольника через основание PK и высоту DH:

$S_{\Delta }=\frac{1}{2}\cdot PK\cdot DH=\frac{1}{2}\cdot 15\cdot DH$

Зная, что площадь равна 45 найдём DH:

$\frac{1}{2}\cdot 15\cdot DH=45\\15\cdot DH=90\\DH=\frac{90}{15}=6$

По теореме Пифагора найдём D₁H в треугольнике в DHD₁:

$D_{1}H=\sqrt{8^{2}+6^{2}}=\sqrt{100}=10$

Находим cos∠DHD₁:

$cos\angle DHD_{1}=\frac{DH}{D_{1}H}=\frac{6}{10}=0,6$

Ответ: 0,6.