Решение заданий варианта №17 из сборника ОГЭ 2024 по математике под редакцией И.В. Ященко 36 типовых экзаменационных вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
Автомобильное колесо, как правило, представляет из себя металлический диск, с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
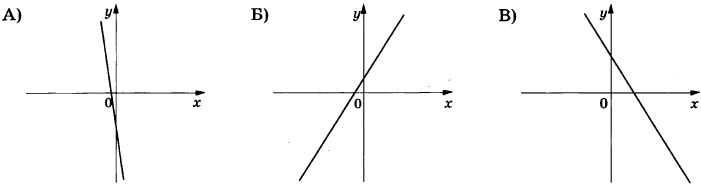
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65R15 (см. рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2).
Второе число (число 65 в приведённом примере) – процентное отношение высоты боковины (параметр Н на рисунке 9) к ширине шины, то есть 100\cdot \frac{H}{B}.
Последующая буква обозначает тип конструкции шины. В данном примере буква R обозначает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяется шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 265/60 R18.
Задание 6.
Найдите значение выражения (\frac{5}{6})^{2}-\frac{11}{45}.
Задание 7.
На координатной прямой точки A, B, C и D соответствуют числам –0,74; –0,047; 0,07; –0,407.
Какой точке соответствует число –0,047?
1) А
2) В
3) С
4) D
Задание 8.
Найдите значение выражения \frac{\sqrt{4a^{11}}\cdot \sqrt{9b^{4}}}{\sqrt{a^{7}b^{4}}} при а = 7 и b = 9.
Задание 9.
Найдите корень уравнения x+\frac{x}{9}=-\frac{10}{3}.
Задание 10.
В сборнике билетов по математике всего 40 билетов, в 18 из них встречается вопрос по теме «Неравенства». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме «Неравенства».
Задание 11.
На рисунках изображены графики функций вида у = kх + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
КОЭФФИЦИЕНТЫ
1) k < 0, b < 0
2) k < 0, b > 0
3) k > 0, b > 0
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 8500 + 6800n, где n – число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 6 колец. Ответ дайте в рублях.
Задание 13.
Укажите решение системы неравенств \begin{cases} x+3,2\le 0, \\ x+1\le -1. \end{cases}
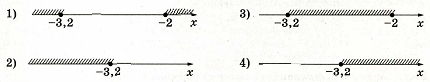
Задание 14.
На клетчатой бумаге с размером клетки 1×1 нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 190.
Задание 15.
На стороне АС треугольника ABC отмечена точка D так, что AD = 6, DC = 8. Площадь треугольника ABC равна 42. Найдите площадь треугольника ABD.
Задание 16.
Угол А четырёхугольника ABCD, вписанного в окружность, равен 37°. Найдите угол С этого четырёхугольника. Ответ дайте в градусах.
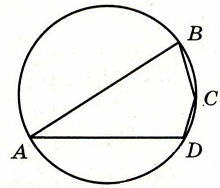
Задание 17.
Найдите площадь ромба, если его диагонали равны 10 и 6.
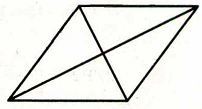
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне АС.
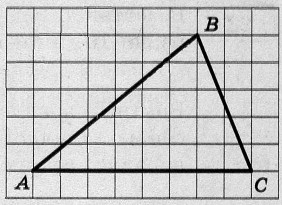
Задание 19.
Какое из следующих утверждений верно?
1) Средняя линия трапеции равна полусумме её оснований.
2) Диагонали любого прямоугольника делят его на четыре равных треугольника.
3) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
В ответ запишите номер выбранного утверждения.
ЧАСТЬ 2
Задание 20.
Решите неравенство -\frac{17}{x^{2}–2x–24}\le 0.
Задание 21.
В сосуд, содержащий 7 литров 26-процентного водного раствора вещества, добавили 6 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Задание 22.
Постройте график функции y=2-\frac{x–5}{x^{2}–5x}.
Определите, при каких значениях m прямая y = m не имеет с графиком общих точек.
Задание 23.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найдите углы ромба.
Задание 24.
Внутри параллелограмма ABCD выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.
Задание 25.
В трапеции ABCD боковая сторона АВ перпендикулярна основанию ВС. Окружность проходит через точки С и D и касается прямой АВ в точке Е. Найдите расстояние от точки Е до прямой CD, если AD = 8, ВС = 7.
Источник варианта: Сборник ОГЭ 2024 по математике. Типовые экзаменационные варианты. 36 вариантов. Проект с участием разработчиков ОГЭ. ФИПИ школе. Авторы-составители: И.В. Ященко, И.Р. Высоцкий, Е.А. Коновалов. Под редакцией И.В. Ященко.