Решение и ответы заданий Варианта №3 из сборника ЕГЭ 2022 по математике (базовый уровень) И.В. Ященко. ГДЗ база для 11 класса. Полный разбор.
Задание 1.
Найдите значение выражения (2\frac{4}{5}-0,8)\cdot 3\frac{1}{8}.
Задание 2.
Каждый день во время конференции расходуется 90 пакетиков чая. Конференция длится 7 дней‚ В пачке чая 100 пакетиков. Какого наименьшего количества пачек чая хватит на все дни конференции?
Задание 3.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) объём железнодорожного вагона Б) объем бытового холодильника В) объём воды в Ладожском озере Г) объём пакета сока | 1) 300 л |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Задание 4.
Результаты соревнований по метанию молота представлены в таблице. 
Места распределяются по результату лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Какое место занял спортсмен Лаптев?
Задание 5.
На фрагменте географической карты схематично изображены очертания Центрального пруда города Одинцово с островом (площадь одной клетки равна 400 м2). Оцените приближённо площадь Центрального пруда, включая остров. Ответ дайте в квадратных метрах. 
Задание 6.
Магазин делает пенсионерам скидку. Десяток яиц стоит в магазине 70 рублей, а пенсионер заплатил за них 65 рублей 10 копеек. Сколько процентов составила скидка для пенсионера?
Задание 7.
Найдите значение выражения \frac{4}{3}\sqrt{6}\cdot \sqrt{54}.
Задание 8.
Радиус окружности, описанной около треугольника, можно вычислить по формуле R=\frac{a}{2\sin \alpha }, где a – сторона, α – противолежащий ей угол треугольника. Пользуясь этой формулой, найдите радиус , если a = 8 и sinα = \frac{1}{5}.
Задание 9.
Найдите корень уравнения log0,4(4x + 10) – log0,40,2 = log0,48.
Задание 10.
Дачный участок имеет форму прямоугольника со сторонами 22 и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
Задание 11.
В фирме такси в наличии 20 легковых автомобилей: 11 из них чёрного цвета с жёлтыми надписями на боках, остальные – жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Задание 12.
Семья из трёх человек планирует поехать из Москвы в Чебоксары. Можно ехать поездом, а можно – на своей машине. Билет на поезд на одного человека стоит 1615 рублей. Автомобиль расходует 9 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина 48 рублей за литр. Сколько рублей придётся заплатить за наиболее дешёвую поездку на троих?
Задание 13.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Задание 14.
На графике изображена зависимость частоты пульса гимнаста от времени в течение и после его выступления в вольных упражнениях. На горизонтальной оси отмечено время (в минутах), прошедшее с начала выступления гимнаста, на вертикальной оси – частота пульса (в ударах в минуту). Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику пульса гимнаста на этом интервале.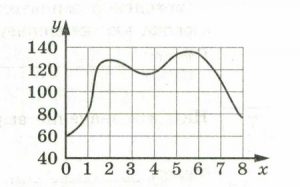 
| ИНТЕРВАЛЫ | ХАРАКТЕРИСТИКИ |
| А) 2-3 мин. Б) 3-4 мин. В) 4-5 мин. Г) 5-6 мин. | 1) частота пульса росла на всём интервале 2) частота пульса достигла максимума за всё время выступления и после него 3) частота пульса сначала падала, а затем росла 4) частота пульса снижалась на всём интервале |
В таблице под каждой буквой укажите соответствующий номер.
Задание 15.
На окружности радиуса √10 отмечена точка C. Отрезок AB – диаметр окружности, AC = 6. Найдите BC.
Задание 16.
Сторона основания правильной шестиугольной пирамиды равна 10, боковое ребро равно 13. Найдите площадь боковой поверхности этой пирамиды. 
Задание 17.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) (x – 1)2(x – 6) < 0 Б) \frac{x-1}{x-6}>0 В) (x – 1)(x – 6) < 0 Г) \frac{(x-6)^{2}}{x-1}>0 | 1) 1 < x < 6 2) x < 1 или x > 6 3) x < 1 или 1 < x < 6 4) 1 < x < 6 или x > 6 |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий решению номер.
Задание 18.
В классе учатся 30 человек, из них 20 человек посещают кружок по биологии, а 16 – кружок по географии. Выберите утверждения, которые верны при указанных условиях.
1) Найдутся хотя бы двое из этого класса, кто посещает оба кружка.
2) Если ученик из этого класса ходит на кружок по биологии, то он обязательно ходит на кружок по географии.
3) Каждый ученик из этого класса посещает оба кружка.
4) Не найдётся 17 человек из этого класса, которые посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 19.
На шести карточках написаны цифры 2; 5; 7; 8; 9; 9 (по одной цифре на каждой карточке). В выражении 
вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20. В ответе укажите, какую-нибудь одну такую сумму.
Задание 20.
Дорога между пунктами A и B состоит из подъёма и спуска, а её длина равна 26 км. Турист прошёл путь из A и B за 6 часов, из которых спуск занял 4 часа. На подъёме скорость туриста на 2 км/ч меньше скорости на спуске. Найдите скорость туриста на спуске. Ответ дайте в км/ч.
Задание 21.
На ленте по разные стороны от середины отмечены две тонкие поперечные полоски: синяя и красная. Если разрезать ленту по красной полоске, то одна часть будет на 25 см длиннее другой. Если разрезать ленту по синей полоске, то одна часть будет на 5 см длиннее другой. Найдите расстояние (в сантиметрах) между красной и синей полосками.
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика базовый уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 30 вариантов.