Решение и ответы заданий № 1–12 варианта №323 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
В течение года произошло три понижения цены товара, причем на 30% каждый раз. Найти конечную цену товара, если первоначально он стоил 100000 рублей.
Задание 2.
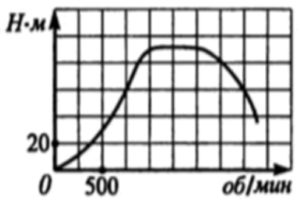
На графике изображена зависимость крутящего момента двигателя катера от числа его оборотов. На оси абсцисс откладывается число оборотов двигателя в минуту, на оси ординат – крутящий момент в Н∙м. Скорость этого катера, измеренная в км/ч, выражается формулой v = 0,04·n, где n – число оборотов двигателя в минуту. Какую наименьшую скорость (в км/ч) должен иметь катер, чтобы крутящий момент его двигателя был не меньше 60 Н∙м?
Задание 3.
Сторона квадрата АВCD равна 6. Найдите скалярное произведение векторов и
.
Задание 4.
Павел Иванович регистрирует автомобиль и получает новый трехзначный номер. Все три цифры нового номера случайны (номер 000 не разрешен). Найдите вероятность того, что при случайном выборе в новом номере все три цифры будут одинаковы. Результат округлить до тысячных.
Задание 6.
Угол при вершине равнобедренного треугольника равен 120°. Боковая сторона равна 4. Найдите квадрат длины медианы, проведенной к боковой стороне.
Задание 7.
Прямая y = 7x + 28 является касательной к графику функции y = ax2 – 21x + 3a. Найдите значение коэффициента a, если известно, что абсцисса точки касания положительна.
Задание 8.
Сторона основания правильной двенадцатиугольной пирамиды равна 6tg15°, а высота равна 4. Найдите расстояние от центра основания пирамиды до плоскости содержащей боковую грань пирамиды.
Задание 10.
Скорость колеблющегося на пружине груза меняется по закону (см/с), где t – время в секундах. Какую долю времени из первых двух секунд скорость движения превышала 3,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Задание 11.
Две копировальные машины печатают рукопись. Если всю рукопись будет печатать первая машина, то работа будет выполнена на 4 минуты позже, чем две машины, работая вместе. Если печатать всю рукопись будет вторая машина, то она напечатает на 25 минут позже, чем обе машины, работая вместе. За сколько минут может напечатать эту рукопись вторая машина?
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 2 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.