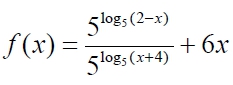Решение и ответы заданий № 1–12 варианта №322 Александра Ларина. Разбор ЕГЭ 2020 по математике (профильный уровень).
Задание 1.
Стрекоза и муха двигаются по прямой. Стрекоза догоняет муху, их скорости равны 1,2 м/с и 30 см/с. Через сколько секунд расстояние между насекомыми сократится с 6,5 м до 20 см?
Задание 4.
На отрезке [‐7; 18] числовой оси случайным образом отмечают одну точку. Найти вероятность того, что координата отмеченной точки будет больше -5, но меньше 9.
Задание 5.
Решите уравнение |x2 – 8x + 5| = 2x . Если уравнение имеет более одного корня, в ответе укажите больший рациональный корень.
Задание 7.
При движении тела по прямой расстояние S (в метрах) до точки отсчета изменялось по закону: S(t) = 5t2 – t3 + 9t, где t – время в секундах, прошедшее от начала движения. Через сколько секунд после начала движения ускорение тела было равно 1 м/с2?
Задание 8.
В прямоугольном параллелепипеде АВСDA1В1С1D1 известны отношения длин ребер: АВ : AD : AA1 = 16 : 15 : 34. Расстояние от центра грани АВВ1A1 до вершины D равно 34√2. Найдите сумму длин всех ребер параллелепипеда.
Задание 10.
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U = U0sin(ωt + φ), где t – время (в секундах), амплитуда напряжения U0 = 2B, частота ω = 2π/3, фаза φ = π/12. Датчик настроен так, что если напряжение U в нем не ниже чем 1 В, загорается лампочка. Какую часть времени, в процентах, на протяжении первой секунды после начала работы лампочка будет гореть?
Задание 11.
На вагоноремонтном заводе в определенный срок должно быть отремонтировано 330 вагонов. Перевыполняя план ремонта в среднем на 3 вагона в неделю, на заводе уже за две недели до срока отремонтировали 297 вагонов. Сколько вагонов в неделю ремонтировали на заводе?
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.3 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.