Сторона основания правильной двенадцатиугольной пирамиды равна 6tg15°, а высота равна 4. Найдите расстояние от центра основания пирамиды до плоскости содержащей боковую грань пирамиды.
Решение:
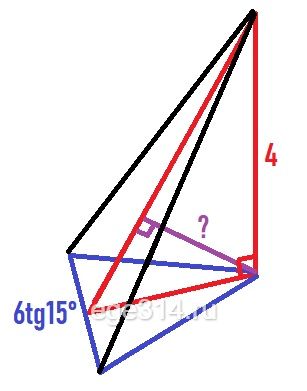
Изобразим часть правильной двенадцатиугольной пирамиды:
Нам необходимо найти фиолетовый перпендикуляр проведённый к апофеме грани пирамиды.
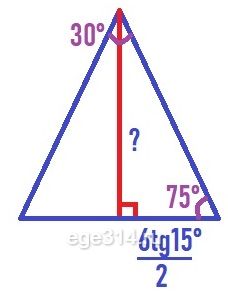
Рассмотрим синий треугольник (из начального рисунка). Он равнобедренный, угол вершины, по свойству правильной пирамиды равен:
360/12 = 30º
Углы при основании равны по:
(180° – 30°)/2 = 75º
Найдём высоту этого треугольника, через тангенс угла:
tg75°=\frac{x}{\frac{6tg15°}{2}}\\tg75°=\frac{x}{3tg15°}\\{\color{Red} x}=tg75°\cdot 3tg15°=tg(90°-15°)\cdot 3tg15°=ctg15°\cdot 3tg15°=3\cdot 1=3
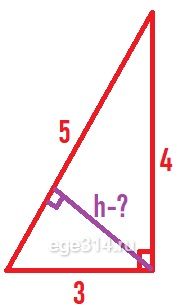
Рассмотрим красный треугольник (из начального рисунка):
Он прямоугольный, в нём мы знаем две стороны 3 и 4, тогда третья сторона равна 5, т.к. это египетский треугольник (или по т.Пифагора).
Через формулу площади треугольника, найдём фиолетовый перпендикуляр, который будет являться высотой этого треугольника:
S_{\Delta}=\frac{1}{2}\cdot 4\cdot 3=6\\S_{\Delta}=\frac{1}{2}\cdot h\cdot 5=6\\2,5\cdot h=6\\{\color{Magenta} h}=\frac{6}{2,5}=2,4
Ответ: 2,4.