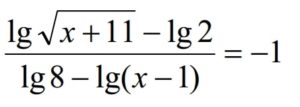Решение и ответы заданий № 1–12 варианта №328 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
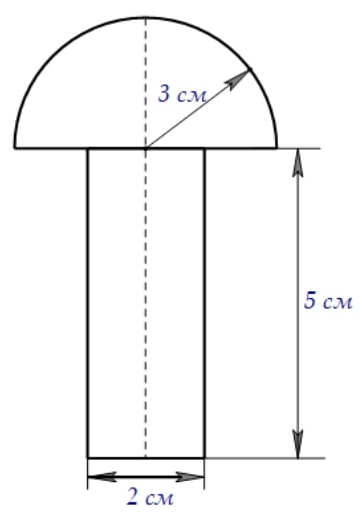
В лифтах развесили рекламные афиши размером 3 дм х 5 дм. Сколько рублей получит владелец лифтов за одну рекламную афишу, если за каждый 1 см2 предоставленной для рекламы площади он получит 50 рублей, а на каждой афише прямоугольник 5 см х 15 см занимает служебная информация, на которой рекламу не размещают?
Задание 4.
Производительности трех станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что ровно одна из них обработана на 3‐м станке?
Задание 6.
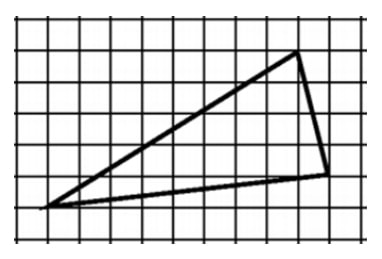
В равнобедренную трапецию вписана окружность. Известно, что боковая сторона трапеции точкой касания делится на отрезки длиной 4 и 1. Найдите площадь трапеции.
Задание 7.
Найдите угловой коэффициент касательной к графику f(x) = 2e5x – 2 + 5x3 функции в точке с абсциссой x0 = 0,4.
Задание 9.
Найдите значение выражения log5(7x4) – log25(49x2), если
Задание 10.
Скейтбордист прыгает на стоящую на рельсах платформу со скоростью v = 5 м/с под острым углом к рельсам. От толчка платформа начинает ехать со скоростью м/с, где m = 70 кг – масса скейтбордиста со скейтом, а M = 430 кг – масса платформы. Под каким максимальным углом α (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,35 м/с?
Задание 11.
На склад 3 машины привезли лук, картошку и капусту. Во второй машине было 200 кг овощей, при этом, лука в 3 раза больше, картошки в 2 раза больше, а капусты в 6 раз больше, чем в первой машине. В третьей машине было 260 кг овощей, при этом, по сравнению со второй машиной, лука было столько же, картошки в 2,5 раза больше, капусты на 9 кг меньше. Сколько килограммов картошки было в первой машине?
Задание 12.
Найдите наибольшее значение функции f(x) = cos2 x + sin x на отрезке [0;]
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.