Досрочный вариант №2 ЕГЭ (профильный уровень) 2020 год

Решение заданий 1–13,15,17,18 варианта №1 досрочного периода ЕГЭ 2020 по математике (профильный уровень).

Задание 1.

Шоколадка стоит 30 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за три шоколадки, покупатель получает четыре (одну в подарок). Какое наибольшее количество шоколадок можно получить, потратив не более 140 рублей в воскресенье?

Задание 2.

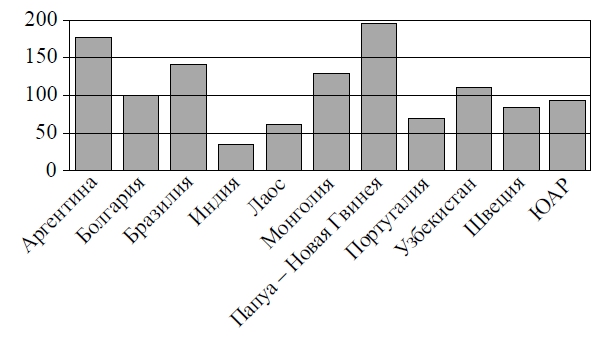
На диаграмме показано распределение выплавки меди в 11 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимала Папуа–Новая Гвинея, одиннадцатое место — Индия. Какое место занимала Болгария?

Задание 3.

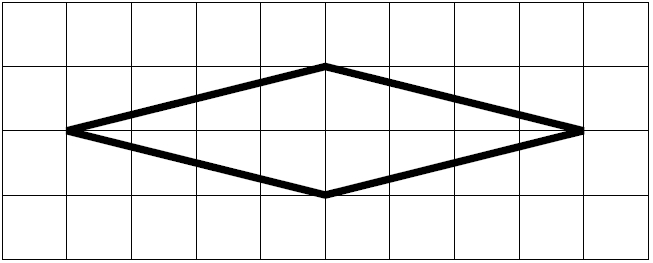
На клетчатой бумаге с размером 1х1 изображён ромб. Найдите его площадь.

Задание 4.

Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8°С, равна 0,91. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8° или выше.

Задание 5.
Найдите корень уравнения log₃ (15-x) = log₃ 7

Задание 6.

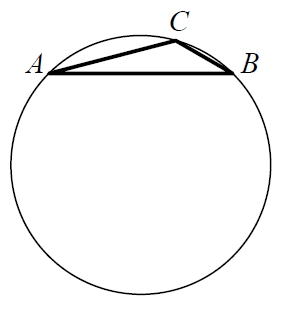
В треугольнике ABC сторона AB равна 2√3, угол C равен 120 градусов. Найдите радиус описанной около этого треугольника окружности.

Задание 7.

На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

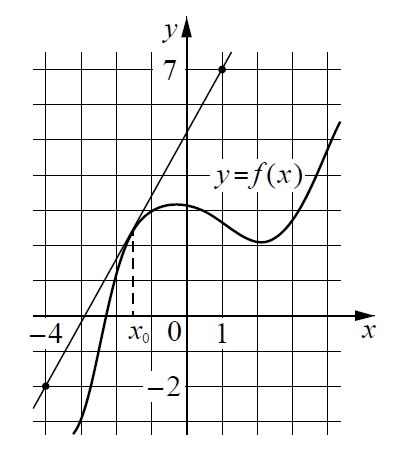
Задание 8.

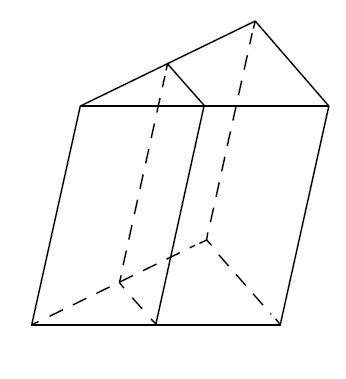
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 7.

Задание 9.
Найдите значение выражения:

$\frac{(3\sqrt{8})^{2}}{6}$

Задание 10.

Два тела, массой m = 6 кг каждое, движутся с одинаковой скоростью v = 9 м/с под углом 2α друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле Q = mv²sin²α, где m — масса (в кг) v — скорость (в м/с). Найдите, под каким углом 2α должны двигаться тела, чтобы в результате соударения выделилось энергия, равная 243 Дж. Ответ дайте в градусах.

Задание 11.

Имеются два сплава. Первый сплав содержит 45% меди, второй – 20% меди. Масса первого сплава больше массы второго на 30 кг. Из этих двух сплавов получили третий сплав, содержащий 40% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Задание 12.
Найдите точку минимума функции y = x^3/2 – 21х + 11.

Задание 13.
а) Решите уравнение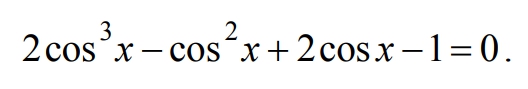

б) Укажите корни этого уравнения, принадлежащие отрезку

Задание 15.
Решите неравенство: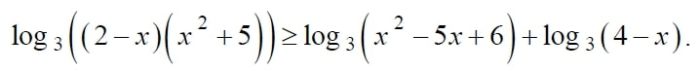

Задание 17.
В июле планируется взять кредит в банке на сумму 10 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 15 млн рублей?

Задание 18.

Найдите все значения a, при каждом из которых уравнение

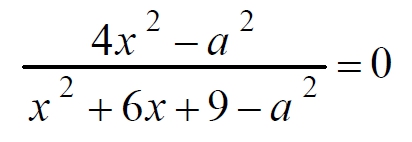
имеет ровно два различных корня.

Источник варианта: fipi.ru