Решение и ответы заданий варианта МА2310201 СтатГрад 13 декабря 2023 года ЕГЭ 2024 по математике (базовый уровень). Тренировочная работа №2. ГДЗ профиль для 11 класса. Полный разбор.
Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в учебных целях.
Задание 1.
В пачке 250 листов бумаги формата А4. За неделю в офисе расходуется 800 листов. Какого наименьшего количества пачек бумаги хватит на 7 недель?
Задание 2.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) расстояние между соседними троллейбусными остановками Б) расстояние от Земли до Луны В) расстояние от Москвы до Сочи Г) диаметр монеты | 1) 20 мм 2) 300 м 3) 385 000 км 4) 1600 км |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Задание 3.
В таблице показано расписание пригородных электропоездов по направлению Москва Октябрьская – Клин – Тверь.
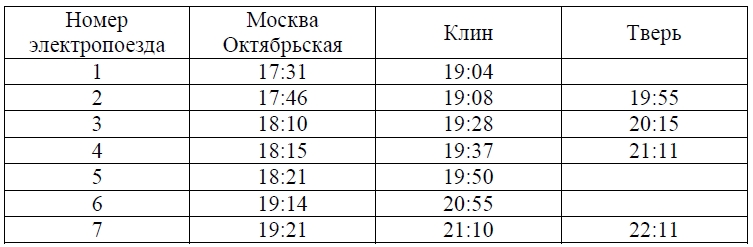
Владислав пришёл на станцию Москва Октябрьская в 18:20 и хочет уехать в Тверь на электропоезде без пересадок. Найдите номер ближайшего электропоезда, который ему подходит.
Задание 4.
Ускорение тела (в м/с2) при равномерном движении по окружности можно вычислить по формуле a = ω2R, где ω – угловая скорость вращения (в с−1), а R – радиус окружности (в метрах). Пользуясь этой формулой, найдите a (в м/с2), если R = 4 м и ω = 7 с−1.
Задание 5.
Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 18 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
Задание 6.
Турист подбирает экскурсии. Сведения об экскурсиях представлены в таблице.
Пользуясь таблицей, подберите набор экскурсий так, чтобы турист посетил четыре объекта: крепость, загородный дворец, парк и музей живописи, а суммарная стоимость экскурсий не превышала 650 рублей. В ответе укажите какой-нибудь один набор номеров экскурсий без пробелов, запятых и других дополнительных символов.
Задание 7.
На рисунке точками показана среднесуточная температура воздуха в Москве в январе 2011 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности точки соединены ломаной линией.
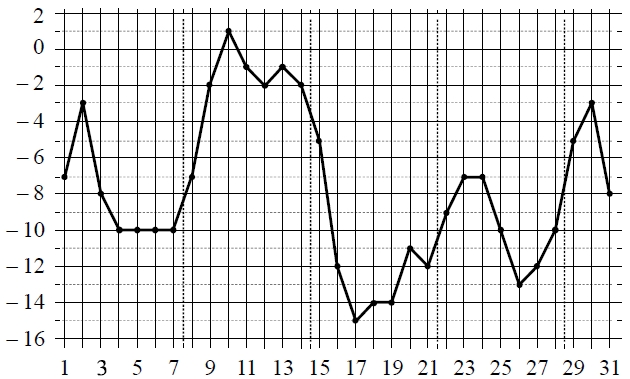
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения температуры.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 1–7 января Б) 8–14 января В) 15–21 января Г) 22–28 января | 1) В конце периода наблюдался рост среднесуточной температуры. 2) В конце периода среднесуточная температура не менялась. 3) Среднесуточная температура достигла месячного минимума. 4) Среднесуточная температура достигла месячного максимума. |
В таблице под каждой буквой укажите соответствующий номер.
Задание 8.
Школа приобрела стол, доску, магнитофон и принтер. Известно, что принтер дороже магнитофона, а доска дешевле магнитофона и дешевле стола. Выберите утверждения, которые верны при указанных условиях.
1) Магнитофон дешевле доски.
2) Принтер дороже доски.
3) Доска – самая дешёвая из покупок.
4) Принтер и доска стоят одинаково.
В ответе запишите номера выбранных утверждений без пробелов, запятых и
других дополнительных символов.
Задание 9.
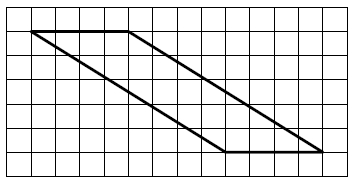
План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
Задание 10.
Дачный участок имеет форму прямоугольника со сторонами 24 метра и 36 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
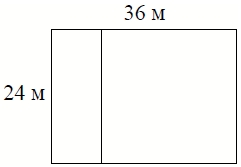
Задание 11.
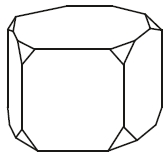
От деревянной правильной пятиугольной призмы отпилили все её вершины (см. рисунок). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Задание 12.
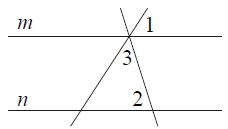
Прямые m и n параллельны (см. рисунок). Найдите ∠3, если ∠1= 74°, ∠2 = 39°. Ответ дайте в градусах.
Задание 13.
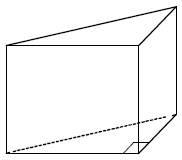
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 2, а гипотенуза равна √29. Найдите объём призмы, если её высота равна 6.
Задание 14.
Найдите значение выражения (\frac{6}{11}+\frac{7}{22}):\frac{19}{44}.
Задание 15.
Цена на электрический чайник была повышена на 19 % и составила 1309 рублей. Сколько рублей стоил чайник до повышения цены?
Задание 16.
Найдите значение выражения \frac{(7^{-3})^{2}}{7^{-9}}.
Задание 17.
Найдите корень уравнения 96 + x = 81.
Задание 18.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) x2 – 6x – 40 ≤ 0 Б) x2 – 13x + 40 ≥ 0 В) x2 + 6x – 40 ≤ 0 Г) x2 + 13x + 40 ≥ 0 | 1) (–∞; – 8] ∪ [–5; +∞) 2) [–4; 10] 3) (–∞; 5] ∪ [8; +∞) 4) [–10; 4] |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий решению номер.
Задание 19.
Найдите трёхзначное натуральное число, большее 600, которое при делении и на 4, и на 5, и на 6 даёт в остатке 3 и цифры в записи которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь одно такое число.
Задание 20.
Из городов A и B, расстояние между которыми равно 260 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 2 часа на расстоянии 160 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Задание 21.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева равна 12 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Источник варианта: СтатГрад/statgrad.org.