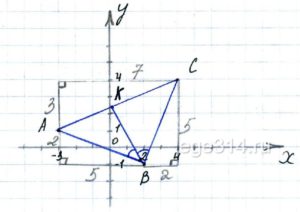
Решение №918 Точки A(-3;1), B(2;-1), C(4;4) являются вершинами треугольника АВС …

Решение:

    Построим по вершинам треугольник АВС:

    Достроив каждую из его сторон до прямоугольного треугольника, видим что катеты одинаковые 2 и 5 клеток. Значит и гипотенузы будут равны, AB = BC.
    Если в треугольнике АВС две стороны равны, то он равнобедренный, а в равнобедренном треугольнике биссектриса ВК является ещё и медианой, тогда:

АК = АС/2

    По теореме Пифагора найдём АС:

АС² = 3² + 7²
АС² = 9 + 49 = 58
АС = √58

    Тогда АК:

AK=\frac{AC}{2}=\frac{\sqrt{58}}{2}

    Найдём 16AK²:

16AK^{2}=16\cdot (\frac{\sqrt{58}}{2})^{2}=16\cdot \frac{58}{4}=\frac{16\cdot 58}{4}=4\cdot 58=232

Ответ: 232.