Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 6. Диагональ параллелепипеда равна 9. Найдите площадь поверхности параллелепипеда.
Решение:
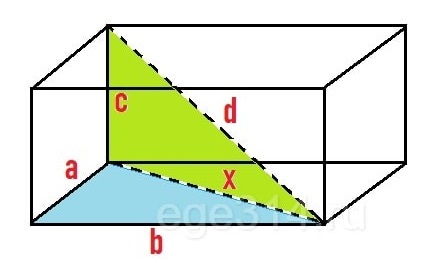
По условию a = 3, b = 6.
Из прямоугольного треугольника найдём диагональ основания (х), по теореме Пифагора:
a2 + b2 = x2
32 + 62 = x2
45 = x2
x = √45
Найдём 3е ребро параллелепипеда из прямоугольного треугольника по теореме Пифагора:
с2 + х2 = d2
с2 = d2 – х2
с2 = 92 – √452
с2 = 81 – 45 = 36
с = 6
По формуле найдём площадь поверхности параллелепипеда:
S = 2•(Sa+ Sb+ Sc) = 2•(ab + bc+ ac) = 2•(3•6 + 6•6 + 3•6) = 144
Ответ: 144.