Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1:2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?
Решение:
V_{кон}=\frac{1}{3}\pi r^{2}h=54
Найдём сначала объём отсечённого конуса. Конус поделен в отношении 1:2, т.е. всего 3 части (1+2), выразим высоту отсечённого конуса:
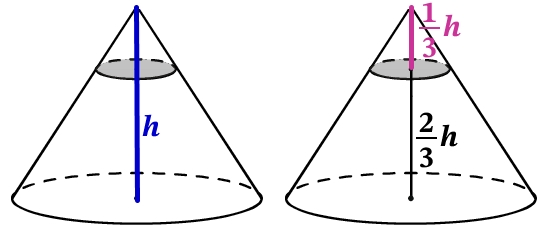
Треугольники подобны по 2-м углам (по прямому и по общему при вершине конуса). Если они подобны и одни стороны (высоты конусов) относятся как \frac{1}{3} то и другие так же (радиусы конусов), поэтому \frac{1}{3} радиуса:
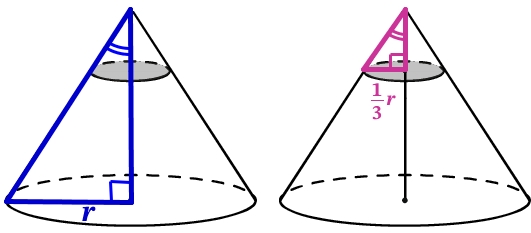
V_{отс}=\frac{1}{3}\cdot \pi\cdot ( \frac{1}{3}r)^{2}\cdot \frac{1}{3}h=\frac{1}{27}\cdot \frac{1}{3}\pi r^{2}h=\frac{1}{27}\cdot V_{кон}=\frac{1}{27}\cdot 54=2
Тогда объём той части исходного конуса, которая примыкает к его основанию равна:
Vосн = V – Vотс = 54 – 2 = 52
Ответ: 52.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.7 / 5. Количество оценок: 166
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.
