Решение:
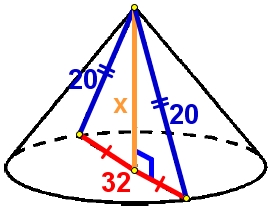
Осевым сечением конуса является равнобедренный треугольник с высотой равной высоте конуса, боковыми рёбрами равными образующими конуса 20.
Основание равнобедренного треугольника, является диаметром конуса и делится высотой на две равных части по 32/2 = 16.
По теореме Пифагора из прямоугольного треугольника найдём высоту осевого сечения:
х2 = 202 – 162
х2 = 400 – 256
х2 = 144
х = √144 = 12
Найдём площадь сечения по формуле площади треугольника:
S_{\Delta }=\frac{1}{2}\cdot {\color{Red} 32}\cdot {\color{Orange} 12}=16\cdot 12=192
Ответ: 192.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 19
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.