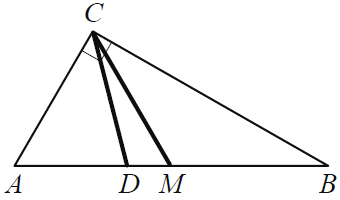
Острый угол B прямоугольного треугольника ABC равен 21°. Найдите величину угла между биссектрисой CD и медианой CM, проведёнными из вершины прямого угла C. Ответ дайте в градусах.
Источник: fipi
Решение:
Т.к. СМ – медиана, то по свойству медианы в прямоугольном треугольнике AМ = МВ = МС. Значит ΔСMB равнобедренный ∠B = ∠BСМ = 21°.
СD – биссектриса, делит прямой ∠С пополам.
Найдём ∠BСD:
∠BСD = ∠С/2 = 90°/2 = 45°
Найдём угол между биссектрисой и медианой:
∠MCD = ∠BСD – ∠BСМ = 45° – 21° = 24°
Ответ: 24.