Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 6. Найдите его большую сторону.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
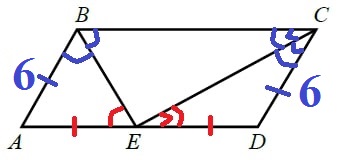
По условию вверху параллелограмма получили две пары равных углов, при делении биссектрисами.
Так же ∠CBE = ∠AEB и ∠BCE = ∠CED, как накрест лежащие углы при пересечении параллельных прямых секущих.
Отсюда, ΔABE и ΔECD равнобедренные. AB = AE = 6, CD = ED = 6.
Найдём большую сторону параллелограмма AD:
AD = AE + ED = 6 + 6 = 12
Ответ: 12.