Угол ACO равен 28°. Его сторона CA касается окружности с центром в точке O. Сторона CO пересекает окружность в точках B и D (см. рис.). Найдите градусную меру дуги AD окружности, заключённой внутри этого угла. Ответ дайте в градусах.
Источники: fipi, os.fipi, Основная волна 2018
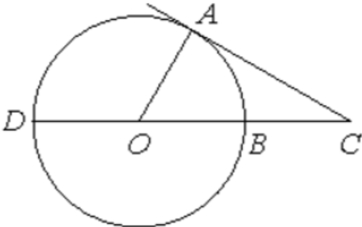
Решение:
ОА – радиус, АС – касательная.
Касательная перпендикулярна радиусу, проведенному в точку касания, тогда ∠А = 90°.
Сумма углов любого треугольника равна 180°. В ΔАОС найдём ∠АОС:
∠АОС = 180° – 90° – 28° = 62°
∠АОС и ∠AOD смежные их сумма равна 180°:
∠AOD = 180° – 62° = 118°
∠AOD – центральный, он равен дуге AD на которую опирается:
‿AD = ∠AOD = 118°
Ответ: 118.