Сторона BC параллелограмма ABCD вдвое больше стороны CD. Точка K – середина стороны BC. Докажите, что DK – биссектриса угла ADC.
Источник: ОГЭ Ященко 2024 (36 вар)
Решение:
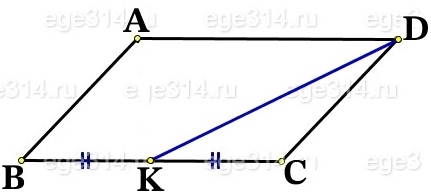
По условию сторона BC параллелограмма АВСD вдвое больше стороны CD.
CD=\frac{BC}{2}=KC
Тогда ΔKCD равнобедренный, углы при основании равны ∠DKC = ∠KDC.
ABCD параллелограмм AB||DC, а DK секущая, ∠DKC = ∠KDA как накрест лежащие.
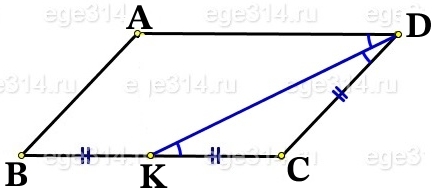
Из двух равенств углов получаем ∠KDC = ∠KDA, значит DK – биссектриса угла АDС.
Что и требовалось доказать.