Окружности с центрами в точках Р и Q не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m : n. Докажите, что диаметры этих окружностей относятся как m : n.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
KH – внутренняя общая касательная к окружностям с центрами в точках P и Q. PQ – отрезок соединяющий центры окружностей.
\frac{PO}{OQ}=\frac{m}{n}
Проведём радиусы окружностей к касательной, по свойству касательной, они будут перпендикулярны:
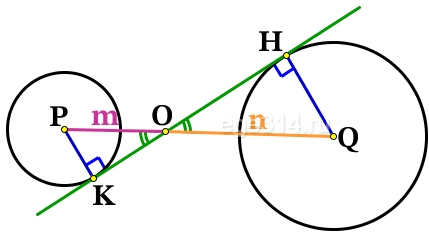
Рассмотрим два прямоугольных ΔPKO и ΔQHO, которые подобны по двум углам (∠POK = ∠HOQ – как вертикальные, ∠PKO = ∠QHO – прямые). В подобных треугольниках, соответствующие стороны пропорциональны:
\frac{PK}{HQ}=\frac{PO}{OQ}\\\frac{PK}{HQ}=\frac{m}{n}
Диаметры окружностей равны (в два раза больше радиусов):
d1 = 2·PK
d2 = 2·HQ
Найдём их отношение:
\frac{d_{1}}{d_{2}}=\frac{2PK}{2HQ}=\frac{PK}{HQ}=\frac{m}{n}
Что и требовалось доказать.