Биссектрисы углов С и D параллелограмма ABCD пересекаются в точке L, лежащей на стороне AB. Докажите, что L – середина AB.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
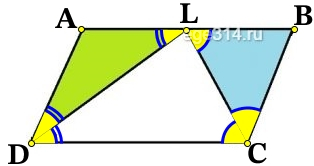
ABCD параллелограмм, поэтому AB||DC.
∠LCD = ∠CLB, как накрест лежащие, при AB||DC и секущей CL. ∠LCD = ∠CLB = ∠LCB, отсюда ΔCLB равнобедренный, LB = CB.
Аналогично, ΔALD равнобедренный, LA = DA.
Стороны DA = CB, как противоположные стороны параллелограмма. Значит, LB = CB = DA = LA, точка L середина стороны AB.
Что и требовалось доказать.