Углы В и С треугольника АВС равны соответственно 65° и 85°. Найдите ВС, если радиус окружности, описанной около треугольника АВС, равен 14.
Источник: ОГЭ Ященко 2024 (36 вар)
Решение:
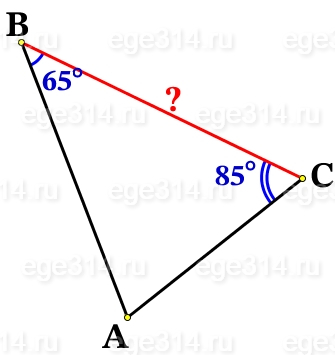
Сумма углов любого треугольника равна 180°. Зная два угла ΔАВС найдём его третий угол:
∠А = 180° – (∠В + ∠С) = 180° – (65° + 85°) = 180° – 150° = 30°
По теореме синусов из справочного материала ОГЭ:
Найдём сторону BC:
\frac{BC}{sin\angle A}=2R\\\frac{BC}{sin30^{\circ} }=2\cdot 14\\\frac{BC}{\frac{1}{2} }=28\\2BC=28\\BC=\frac{28}{2}=14
Ответ: 14.