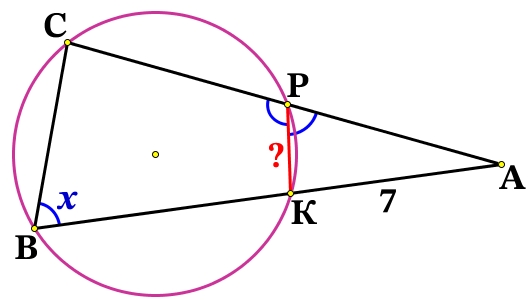
Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АK = 7, а сторона AС в 1,4 раза, больше стороны BC.
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
Четырёхугольник CBKP вписан в окружность, сумма противолежащих углов равна 180°. Пусть ∠В равен х, тогда противолежащий ∠СРК = 180° – х. Угол ∠АРК смежный к ∠СРК, тогда ∠АРК = 180 – (180 – х) = х. Значит ∠АРК = ∠В.
В ΔСАВ и ΔРАК: ∠АРК = ∠В, угол А общий, значит эти треугольники подобны по двум равным углам. Тогда и стороны подобны:
\frac{AK}{AC}=\frac{KP}{BC}
По условию AС = 1,4·ВС, AK = 7, тогда:
\frac{7}{1,4\cdot BC}=\frac{KP}{BC} {|\color{Blue} \cdot BC}\\\frac{7}{1,4}=\frac{KP}{1}\\KP=\frac{7}{1,4}=5
Ответ: 5.