Окружность с центром на стороне АС треугольника АВС проходит через вершину C и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 3,6, а АВ = 8.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
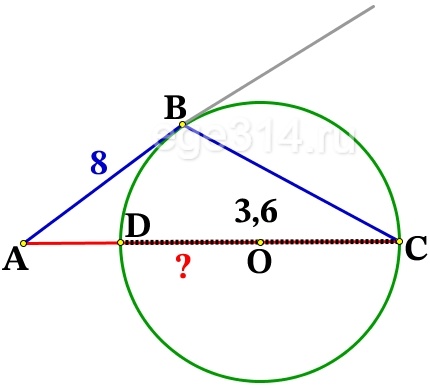
По теореме о секущей и касательной (подробно о ней здесь):
Если из одной точки к окружности проведены секущая (АС) и касательная (АB), то произведение всей секущей (АС) на ее внешнюю часть (АD) равно квадрату отрезка касательной (АB).
АС·АD = АB2
АС·(AC – DC) = 82
АС·(AC – 3,6) = 64
АС2 – 3,6·AC = 64
АС2 – 3,6·AC – 64 = 0
D = (–3,6)2 – 4·1·(–64) = 268,96 = 16,42
AC_{\:1}=\frac{3,6+16,4}{2\cdot 1}=\frac{20}{2}=10\\AC_{\:2}=\frac{3,6–16,4}{2\cdot 1}=\frac{–12,8}{2}\:{\color{Blue} <0\:\notin }
Ответ: 10.