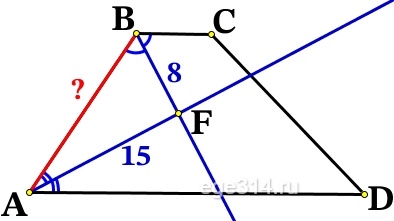
Решение №2685 Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD пересекаются в точке F.

Решение:

    ∠ABC и ∠ВАD односторонние при параллельных прямых AD и ВС и секущей АВ, их сумма равна 180°:

∠ABC  + ∠ВАD = 180°

    ∠АВF и ∠ВАF образованы биссектрисами они равны:

∠АВF = ∠ABC/2
∠ВАF = ∠ВАD/2 

    Тогда их сумма равна:

∠ABC/2 + ∠ВАD/2 = 180°/2
∠АВF + ∠ВАF = 90°

    Сумма углов треугольника равна 180°. В ΔАВF найдём ∠ВFА:

∠ВFА = 180 – (∠АВF + ∠ВАF) = 180° – 90° = 90°

    Значит ΔАВF прямоугольный, тогда по теореме Пифагора, найдём искомую сторону АВ:

АВ² = АF²  + BF²
АВ² = 15² + 8² = 225 + 64 = 289
АВ = √289 = 17

Ответ: 17.