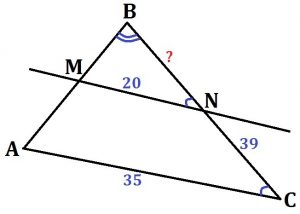
Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если МN = 20‚ АС = 35‚ NС = 39.
Источник задания: ОГЭ 2021 Математика, И.В. Ященко. 36 вариантов.
Решение:
Рассмотрим ΔВМN и ΔАВС, в них ∠В общий, ∠МNB = ∠АСВ, как соответственные при двух параллельных прямых MN||AC и секущей ВС.
ΔВМN и ΔАВС подобны по двум равным углам. Значит пропорциональны соответствующие стороны:
35BN = 20·(BN + 39)
35BN = 20BN + 20·39
35BN – 20BN = 780
15BN = 780
Ответ: 52.