Решение №1645 Биссектриса угла А параллелограмма АВСD пересекает сторону ВС в точке К.

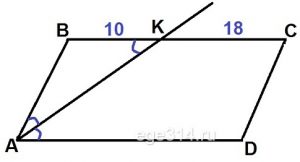
Биссектриса угла А параллелограмма АВСD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 10, СК = 18.

Источник: ОГЭ 2021 Ященко 36 вариантов.

Решение:

Периметр параллелограмма это сумма его 4-х сторон:

P_ABCD = BC + AD + BA + DC

Найдём сторону ВС:

ВС = ВК + КС = 10 + 18 = 28

AD = ВС как противолежащая сторона параллелограмма:

АD = 28

∠АКВ = ∠КАD как накрест лежащие при параллельных прямых ВС||AD и секущей АК.
∠ВАК = ∠КАD, т.к. образованы биссектрисой АК.
Значит, ∠АКВ = ∠ВАК, тогда Δ АВК равнобедренный, в нём боковые стороны равны:

АВ = ВК = 10

AВ = DС как противолежащая сторона параллелограмма:

DC = 10

Найдём периметр параллелограмма:

P = 28 + 28 + 10 + 10 = 76

Ответ: 76.