Решение №4478 Постройте график функции y = |x^2 + 5x + 6|

Постройте график функции y = |x² + 5x + 6| − 1.
Определите, при каких значениях m прямая y = m имеет с графиком ровно общие точки.

Источник: ОГЭ Ященко 2024 (36 вар)

Решение:

Сначала построим график параболы: y = x² + 5x + 6. Найдём координаты вершины параболы:

$x_{верш}=\frac{–b}{2a}=\frac{–5}{2\cdot 1}=-2,5$
y_верш (–2,5) = (–2,5)² + 5·(–2,5) + 6 = –0,25
(–2,5; –0,25) – вершина параболы

x	–4	–3	–2	–1
y	2	0	0	2

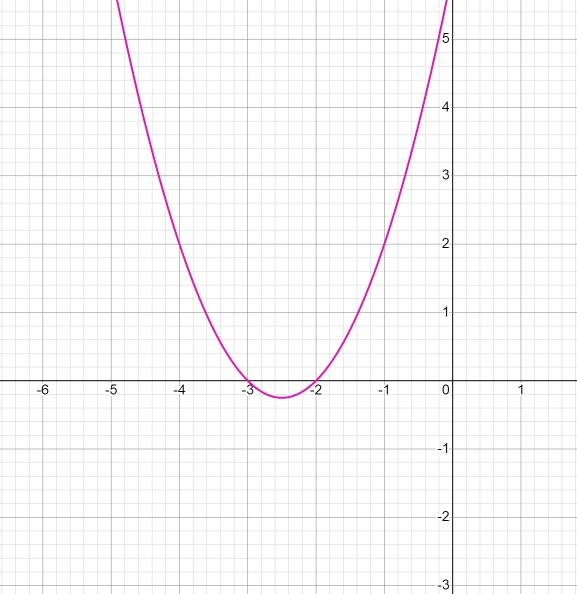
Добавим модуль y = |x² + 5x + 6|, часть параболы, которая ниже y = 0, симметрично отразим выше у = 0:

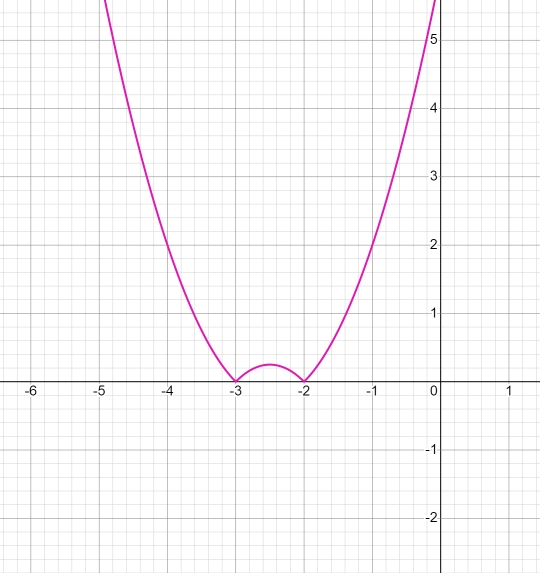
Добавим –1, y = |x² + 5x + 6| − 1, каждую точку графика сдвинем на 1 единицу вниз:

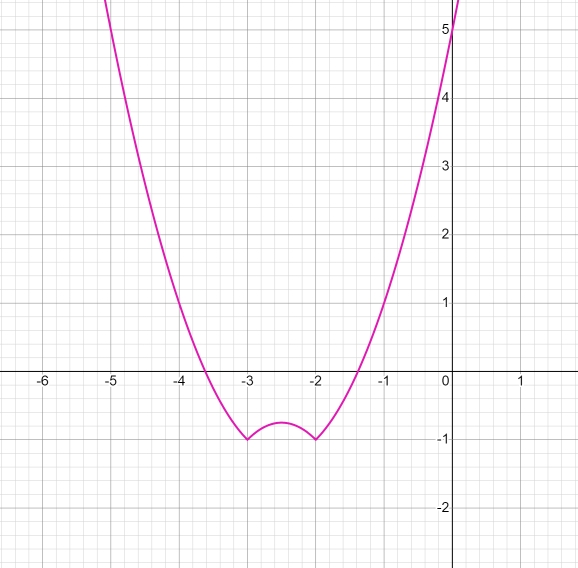
Нарисуем прямые y = m, имеющие с графиком 2 общие точки:

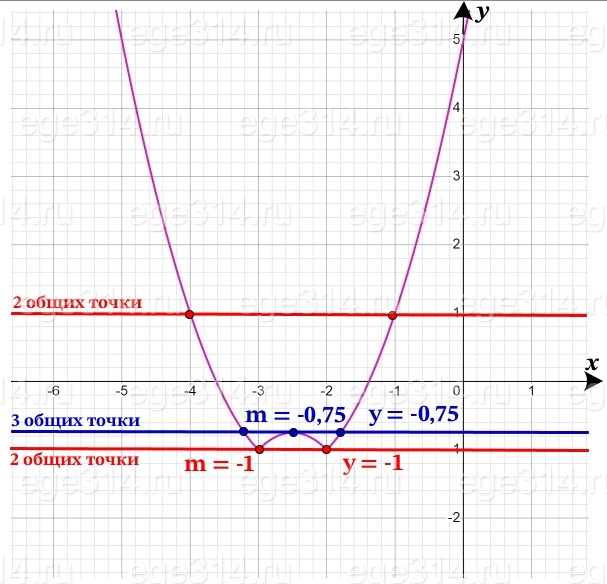
m > –0,75; m = –1.

Ответ: m > –0,75; m = –1.