Решение №4441 Постройте график функции y={x^2+1 при x≥-1, -4/x при x

Постройте график функции

$y=\begin{cases} x^{2}+1 \:\:при\:\:x\ge -1,\\ -\frac{4}{x}\:\:при\:\:x\lt -1. \end{cases}$

Определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.

Источник: ОГЭ Ященко 2024 (36 вар)

Решение:

Парабола:

y = x² + 1, x ≥ –1, ветви направлены вверх (а = +1);

Найдём координаты вершины параболы:

$x_{верш}=\frac{–b}{2a}=\frac{–0}{2\cdot 1}=0$
y_верш (0) = 0² + 1 = 1
(0; 1) – вершина параболы

x	–1	0	1	2
y	2	1	2	5

Прямая:

y = $\color{Green} -\frac{4}{x}$ , x < –1, гипербола II четверть;

(–1; 4) ∉ графику, начало гиперболы;

x	–2	–4	–8
y	2	1	0,5

$Постройте график функции y={x^2+1 при x≥-1, -4/x при x<-1.$

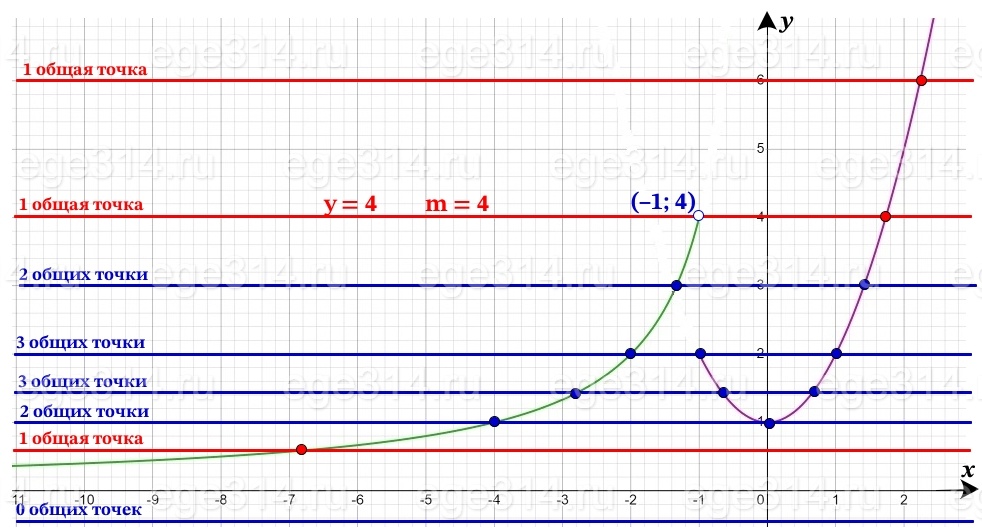
y = m, прямая параллельная оси х или совпадающая с ней.

m ∈ (0; 1) ∪ [4; +∞)

Ответ: (0; 2) ∪ [4; +∞).