Постройте график функции y=\frac{(0,5x^{2}–2x)\cdot |x|}{x–4}.
Определите, при каких значениях m прямая у = m не имеет с графиком ни одной общей точки.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
y=\frac{(0,5x^{2}–2x)\cdot |x|}{x–4}
ограничение: x – 4 ≠ 0
x ≠ 4
y=\frac{(0,5x^{2}–2x)\cdot |x|}{x–4}=\frac{0,5x\cdot (x–4)\cdot |x|}{x–4}=0,5x\cdot |x|=\begin{cases} 0,5x\cdot (+x) \:{\color{Blue} ;x\ge 0} \\ 0,5x\cdot (–x)\:{\color{Blue} ;x<0} \end{cases}=\begin{cases} 0,5x^{2} \:{\color{Blue} ;x\ge 0} \\ -0,5x^{2}\:{\color{Blue} ;x<0} \end{cases}
Найдём координату у точки не принадлежащей графику функции, подставив координата х = 4, в уравнение с условием х ≥ 0:
y(4)=0,5\cdot 4^{2}=0,5\cdot 16=8
А (4; 8) ∉ графику функции
у = 0,5х2; х ≥ 0 – квадратичная функция, график парабола
| x | 0 | 1 | 3 |
| y | 0 | 0,5 | 4,5 |
у = –0,5х2; х < 0 – квадратичная функция, график парабола
| x | –1 | –3 | –4 |
| y | –0,5 | –4,5 | –8 |
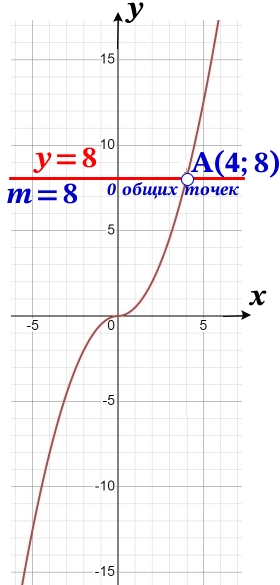
Прямая у = 8 не имеет с графиком ни одной общей точки.
Ответ: m = 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 56
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.
