Решение №4181 Даны точки A(5; 4) и B(6; 3). Найдите скалярное произведение AB и CB, если BC = 9, ∠CBA = 135°.

Решение:

    Найдём координаты вектора АВ:

\overrightarrow{AB}=(6-5;3-4)=(1;-1)

    Найдём длину вектора АВ:

|\overrightarrow{AB}|=\sqrt{1^{2}+(-1)^{2}}=\sqrt{2}

    Построим рисунок по условию задачи и параллельным переносом перенесём вектор СВ, совместив его начало с началом вектора АВ:

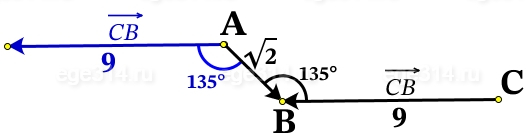
    Найдём скалярное произведение \overrightarrow{AB} и \overrightarrow{CB}:

\overrightarrow{AB}\cdot \overrightarrow{CB}=|\overrightarrow{AB}|\cdot |\overrightarrow{CB}|\cdot cos\alpha=\sqrt{2 }\cdot 9\cdot cos135^{\circ }=\sqrt{2 }\cdot 9\cdot (-\frac{\sqrt{2}}{2})=-\frac{\sqrt{2}^{2}\cdot 9}{2}=-9

Ответ: –9.