Решение №4179 Сторона равностороннего треугольника АВС равна 6√3. Найдите скалярное произведение векторов АВ→ и СА→.

Решение:

    Построим рисунок по условию задачи:

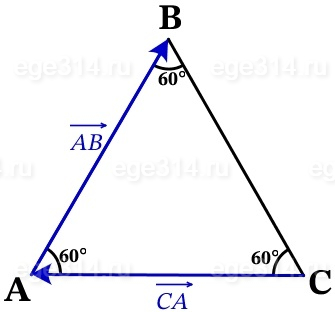
    Перенесём вектор СА так, что бы его начало было в той же точке, что и начало вектора АВ:

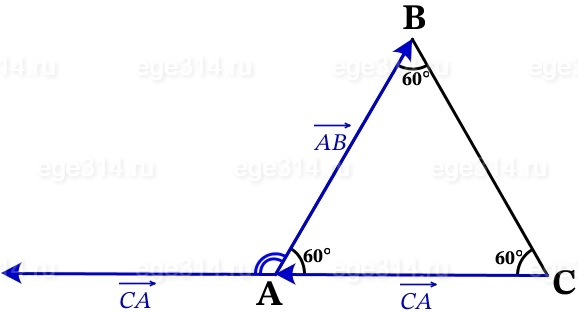
    Найдём угол между векторами, он смежный с углом равностороннего треугольника. Сумма смежных углов всегда равна 180.

α = 180° – 60° = 120°

    Найдём скалярное произведение векторов \overrightarrow{AB} и \overrightarrow{CA}

\overrightarrow{AB}\cdot \overrightarrow{CA}=|\overrightarrow{AB}|\cdot |\overrightarrow{CA}|\cdot cos\alpha=6\sqrt{3}\cdot 6\sqrt{3}\cdot cos120^{\circ }=36\cdot (\sqrt{3})^{2}\cdot (-\frac{1}{2})=36\cdot 3\cdot (-\frac{1}{2})=-54

Ответ: –54.