Сторона равностороннего треугольника ABC равна 6√3. Найдите длину суммы векторов \overrightarrow{AB} и \overrightarrow{AC}.
Источник: ЕГЭп Ященко 2024 (50 вар)
Решение:
Изобразим условие задания:
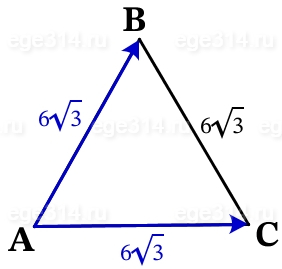
Перенесём параллельным переносом вектор AC в конец вектора АВ:
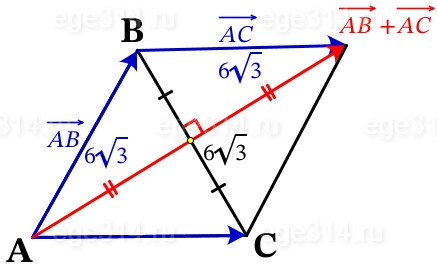
Рисунок можно достроить до ромба, а искомая сумма векторов, будет являться большей диагональю ромба.
В ромбе диагонали пересекаются под прямым углом и в точке пересечения делятся пополам. Половина одной из диагоналей равна:
6√3/2 = 3√3
Половину другой диагонали, найдём по теореме Пифагора из прямоугольного треугольника:
6√32= х2 + 3√32
108 = х2 + 27
108 – 27 = х2
81 = х2
х = √81 = 9
Найдём всю диагональ:
2·х = 2·9 = 18
Ответ: 18.