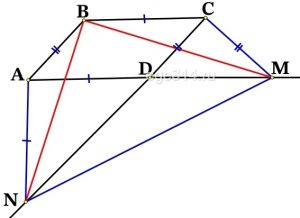
В параллелограмме ABCD угол А острый. На продолжениях сторон AD и CD за точку D выбраны точки М и N соответственно, причём AN = AD и CM = CD.
а) Докажите, что BN = BM.
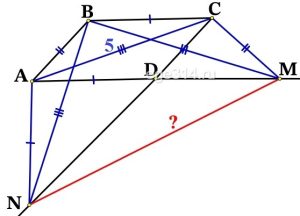
б) Найдите MN, если АС = 5, sin∠BAD = \frac{5}{13}.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
а) Доказать: BN = BM.
Рассмотрим ΔNAB и ΔBCM. В них по условию и как стороны параллелограмма AN = AD = BC, AB = CD = CM. Трапеции NABC (AN = BC) и ABCM (AB = CM) равнобедренные. Углы при верхних основаниях равны (как и при нижних), т.е. в трапеции NABC при основании AB ∠NAB = ∠ABC, в трапеции ABCM при основании BC ∠ABC = ∠BCM, отсюда ∠ANB = ∠BCM.
Значит, ΔNAB = ΔBCM по двум сторонам и углу между ними. Тогда, равны и соответственные стороны BN = BM этих треугольников.
Что и требовалось доказать.
б) Найти MN, если АС = 5, sin∠BAD = \frac{5}{13}.
ABCM и NABC – равнобедренные трапеции, их диагонали равны:
BN = BM = AC = 5
Выразим ∠NBM:
∠NBM = ∠CBA – ∠CBM – ∠NBA = ∠CBA – ∠CBM – ∠BMC = ∠CBA – (180 – ∠BCM) = ∠CBA – (180 – ∠СBA) = 2∠CBA – 180° = 2·(180° – ∠BAD) – 180° = 180° – 2∠BAD
Найдём cos∠NBM:
cos∠NBM = cos(180° – 2∠BAD) = cos180°·cos(2∠BAD) + sin180°·sin(2∠BAD) = –1·cos(2∠BAD) + 0·sin(2∠BAD) = –cos(2∠BAD) = –(cos2∠BAD – sin2∠BAD) = sin2∠BAD – cos2∠BAD = sin2∠BAD – (1 – sin2∠BAD) = sin2∠BAD – 1 + sin2∠BAD = 2sin2∠BAD – 1 = 2·(\frac{5}{13})^{2} – 1 =\frac{2\cdot 25}{169} – 1 = \frac{50}{169}– \frac{169}{169}= –\frac{119}{169}
В ΔNBM по теореме косинусов найдём MN:
MN2 = 52 + 52 – 2·5·5·(-\frac{119}{169})
MN2 = 25 + 25 + 50·\frac{119}{169}
MN2 = 50 + 50·\frac{119}{169}
MN2 = 50·(1 + \frac{119}{169})
MN2 = 50·\frac{288}{169}
MN2 = \frac{14400}{169}
MN=\sqrt{\frac{14400}{169}}=\frac{120}{13}
Ответ: б) \frac{120}{13}.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 48
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.