Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Источник: ОГЭ Ященко 2024 (36 вар)
Решение:
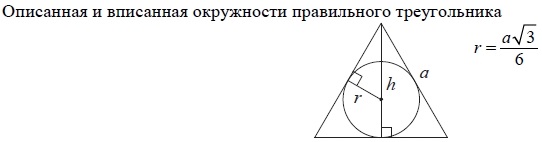
По формуле из справочного материала ОГЭ, найдём сторону треугольника:
r=\frac{a\sqrt{3}}{6}\\10\sqrt{3}=\frac{a\sqrt{3}}{6}\:{\color{Blue} |: \sqrt{3}}\\10=\frac{a}{6}\\a=10\cdot 6=60
Ответ: 60.