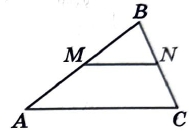
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB = 66, AC = 44, MN = 24. Найдите AM.
Источник: ОГЭ Ященко 2024 (36 вар)
Решение:
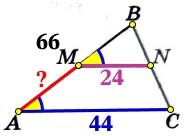
Рассмотрим ΔВМN и ΔАВС, в них ∠В общий, ∠BMN = ∠BAC, как соответственные при двух параллельных прямых MN||AC и секущей ВA.
ΔВМN и ΔАВСподобны по двум равным углам. Значит пропорциональны соответствующие стороны:
\frac{MN}{AC}=\frac{BM}{AB}\\\frac{24}{44}=\frac{BM}{66}\\\frac{6}{11}=\frac{BM}{66}
11·BM = 6·66 |:11
BM = 6·6 = 36
Найдём АМ:
АМ = АВ – ВМ = 66 – 36 = 30
Ответ: 30.