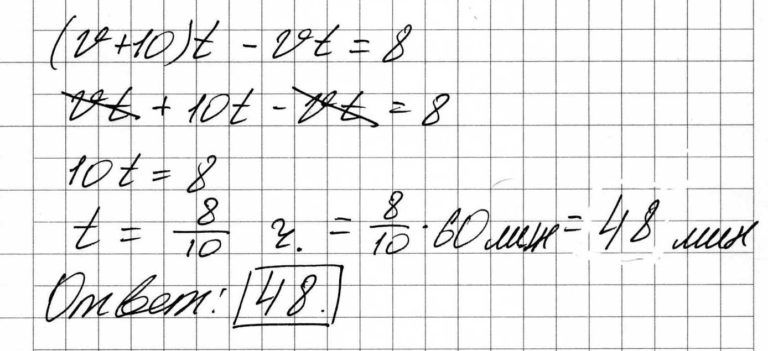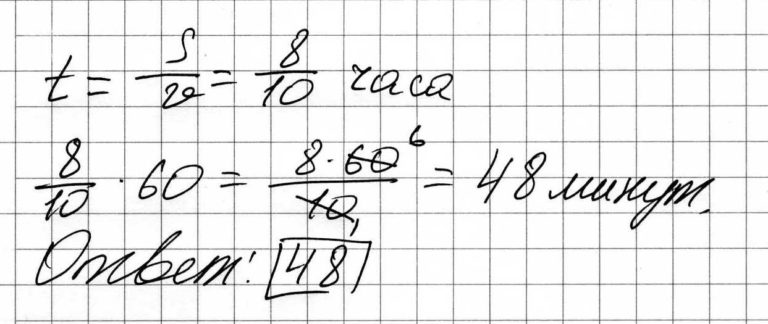Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 16 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 10 км/ч больше скорости другого?
Источник: mathege
Решение №1:
Трасса имеет длину 16 км, тогда расстояние между мотоциклистами 16/2 = 8 км.
Пусть скорость второго v, тогда первого v + 10. Время через которое они поравняются обозначим t. Расстояние пройденное первым (v + 10)·t, а вторым v·t. Составим уравнение:
Ответ: 48.
Решение №2:
Трасса имеет длину 16 км, тогда расстояние между мотоциклистами 16/2 = 8 км. Разница в скорости будет скоростью сближения, т.е. 10 км/ч. Тогда время находится так:
Ответ: 48.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 10
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.