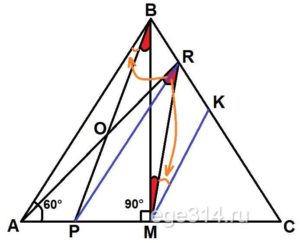
Точка M – середина стороны AC равностороннего треугольника ABC. Точки P и R на отрезках AM и BC соответственно выбраны так, что AP = BR. Найдите сумму углов ARM, PBM и BMR.
Источник: XIII математическая олимпиада им. Л. Эйлера
Решение:
Построим по условию ΔАВС и достроим в нём прямую PR (получим равнобедренную трапецию АВКР), и среднюю линию МК:
Необходимо найти сумму углов:
∠ARM + ∠PBM + ∠BMR
∠ARM разобьём на два угла:
∠ARM = ∠ARP + ∠PRM
∠PRM = ∠RMK как накрест лежащие при PR||MK и секущей MR
∠ARP = ∠BAR как накрест лежащие при AB||PR и секущей AR
∠BAR = ∠BAO = ∠ABO, как углы при основании равнобедренного ΔАОВ (образованный диагоналями равнобедренной трапеции ABRP)
Значит, ∠ARP = ∠ABO
Тогда наша искомая сумма углов, принимает вид:
∠ARM + ∠PBM + ∠BMR = ∠ARP + ∠PRM + ∠PBM + ∠BMR = ∠ABO + ∠RMK + ∠PBM + ∠BMR = ∠АВМ + ∠BMK
∠АВМ = ∠BMK как накрест лежащие при AB||КМ и секущей ВМ
Рассмотрим ΔАВМ, в нём ∠ВАМ = 60°, как угол равностороннего ΔАВС, ∠АМВ = 90°, т.к. ВМ это медиана и высота равностороннего ΔАВС, найдём ∠АВМ:
∠АВМ = 180° – ∠ВАМ – ∠АМВ = 180° – 60° – 90° = 30°
Искомая сумма углов равна:
∠АВМ + ∠BMK = ∠АВМ + ∠АВМ = 30° + 30° = 60°
Ответ: 60.
Ещё одна задача из этой олимпиады здесь.