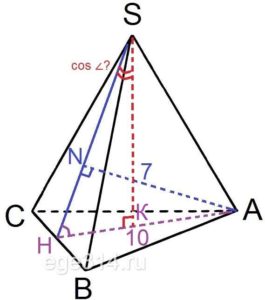
Расстояние от вершины основания правильной треугольной пирамиды до плоскости боковой грани, не содержащей эту вершину, равно 7. Высота основания пирамиды равна 10. Найдите косинус угла между высотой пирамиды и апофемой.
Решение:
Расстояние от вершины B основания правильной треугольной пирамиды, до плоскости боковой грани – это расстояние до апофемы SH этой боковой грани.
В прямоугольном ΔАNH найдём sin ∠NHA:
sin\angle NHA=\frac{NA}{HA}=\frac{7}{10}=0,7
Выразим ∠HSK в прямоугольном ΔHSK:
∠HSK = 180º – 90º – ∠NHA = 90º – ∠NHA
В прямоугольном ΔАNH найдём cos ∠HSK:
cos ∠HSK = cos (90º – ∠NHA) = sin ∠NHA = 0,7
(по формулам приведения)
Ответ: 0,7.