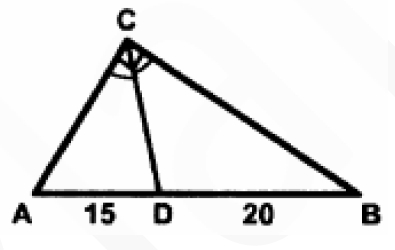
Найдите площадь прямоугольного треугольника АВС, изображенного на рисунке. CD – биссектриса угла АСВ.
Решение:
По теореме биссектриса в треугольнике делит противоположную сторону на части, пропорциональные прилежащим сторонам.
\frac{CA}{CB}=\frac{AD}{DB}=\frac{15}{20}=\frac{3}{4}
Пусть CA = 3x , а CB = 4x, тогда по теореме Пифагора гипотенуза:
AB=\sqrt{CA^{2}+CB^{2}}=\sqrt{(3x)^{2}+(4x)^{2}}=\sqrt{25x^{2}}=5x
По условию длина гипотенузы:
AB = AD + DB = 15 + 20 = 35
Таким образом, 5x = 35, откуда x = 7
Тогда CA = 3·7 = 21, CB = 4·7 = 28
Площадь треугольника равна:
S_{ABC}=\frac{1}{2}\cdot CA\cdot CB=\frac{1}{2}\cdot 21\cdot 28=294
Ответ: 294.