Решение:
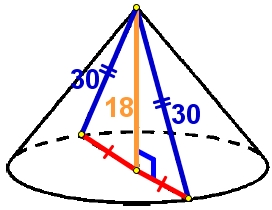
Осевым сечением конуса является равнобедренный треугольник с высотой равной высоте конуса 18, боковыми рёбрами равными образующими конуса 30.
Основание равнобедренного треугольника делится высотой на две равных части х, найдём одну из них по теореме Пифагора из прямоугольного треугольника:
х2 = 302 – 182
х2 = 900 – 324
х2 = 576
х = √574 = 24
Тогда всё основание равно:
2х = 2·24 = 48
Найдём площадь сечения по формуле площади треугольника:
S_{\Delta }=\frac{1}{2}\cdot {\color{Red} 48}\cdot {\color{Orange} 18}=24\cdot 18=432
Ответ: 432.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.4 / 5. Количество оценок: 22
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.