На рисунке изображён график y = f ‘(x) – производной функции f(x), определённой на интервале (−6; 5). В какой точке отрезка [−5; −2] функция f(x) принимает наименьшее значение?
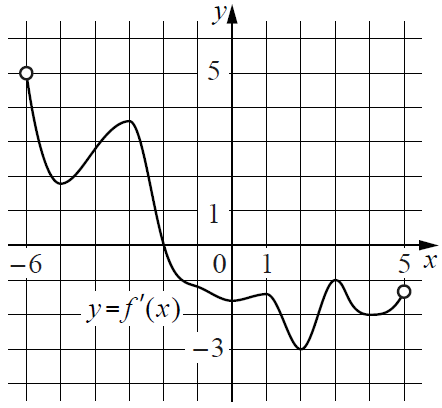
Источник: fipi
Решение:
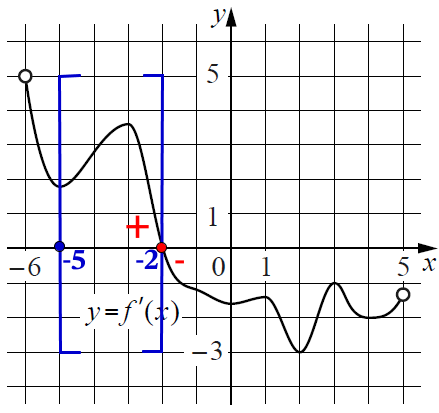
Дан график производной функции. На отрезке [–5; –2] точка х = –2 точка максимума, т.к. знак производной меняется с + на –, здесь функция принимает наибольшее значение.
Значит на всём отрезке до этой точки, функция возрастает, наименьшее значение будет в крайней левой точке, это х = –5.
Ответ: –5.