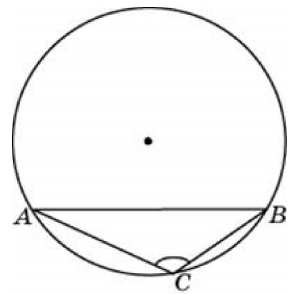
Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиусом 35√3.
Источник: statgrad
Решение:
Пользуемся формулой расширенной теоремы синусов:
\frac{a}{sin\alpha}=2R\\\frac{AB}{sin120^{\circ }}=2\cdot 35\sqrt{3}\\\frac{AB}{\frac{\sqrt{3}}{2}}=70\sqrt{3}\\AB=\frac{\sqrt{3}}{2}\cdot 70\sqrt{3}=\frac{\sqrt{3 }\cdot 70\cdot \sqrt{3}}{2}=\frac{\sqrt{9}\cdot 35}{1}=\frac{3\cdot 35}{1}=105
Ответ: 105.