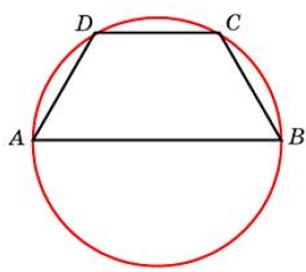
Решение:
По условию:
∠A = 60°
∠A и ∠D односторонние при двух параллельных прямых и секущей их сумма равна 180°:
∠D = 180° – ∠A = 180° – 60° = 120°
По условию:
AD = DC = CB
Отсюда ΔADC равнобедренный, углы при основании равны, найдём их:
Найдём ∠АСВ:
∠АСВ = ∠С – ∠АСD = 120° – 30° = 90°
Тогда вписанный в окружность ΔАВС прямоугольный, а значит его гипотенуза АВ является диаметром окружности, найдём радиус:
R = d/2 = 38/2 = 19
Ответ: 19.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.6 / 5. Количество оценок: 8
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.