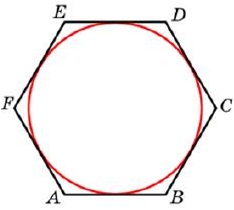
Решение №2076 Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 10√3.

Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 10√3.

Источник: mathege

Решение:

Вся окружность равна 360°, тогда радиусами проведённым к вершинам шестиугольника, делится на углы равные:

∠АОВ = 360°/6 = 60°

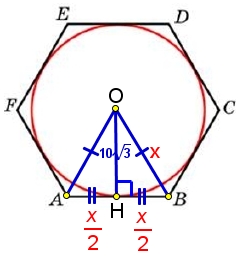
Тогда ΔАОВ равносторонний, ОН – высота, тогда АВ/2 = АН = НВ.
Пусть ОВ равен х, тогда НВ равен $\frac{x}{2}$ , по теореме Пифагора найдём ОВ:

$OB^{2}=OH^{2}+HB^{2}$

$x^{2}=(10\sqrt{3})^{2}+(\frac{x^{}}{2})^{2}$

$x^{2}=300+\frac{x^{2}}{4}$ |·4

4x² = 1200 + x²
3x² = 1200
x² = 1200/3 = 400
x = √400 = 20

ОВ = АВ, как стороны равностороннего треугольника, АВ = 20 – сторона правильного шестиугольника.

Ответ: 20.