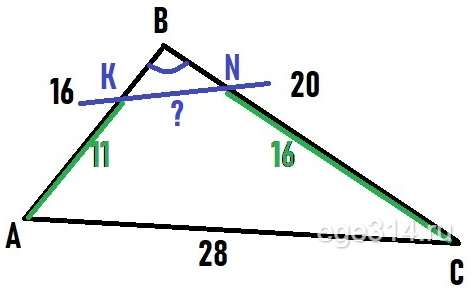
Прямая пересекает стороны АВ и ВС треугольника АBС в точках К и N соответственно. Известно, что АВ = СN = 16, ВС = 20, АС = 28, АК = 11. Найдите длину отрезка КN.
Решение:
В треугольнике ΔBNK найдём стороны BK и BN:
BK = BA – AK = 16 – 11 = 5
BN = BC – CN = 20 – 16 = 4
Рассмотрим треугольники ΔBNK и ΔBAC, в них угол ∠В общий. Мысленно перевернём ΔBNK и поменяем местами стороны BK и BN.
Cторона BK относится к стороне BC как:
\frac{BK}{BC}=\frac{5}{20}=\frac{1}{4}
Cторона BN относится к стороне BA как:
\frac{BN}{BA}=\frac{4}{16}=\frac{1}{4}
Коэффициент подобия один, значит треугольники подобны, тогда подобны и третьи стороны:
\frac{KN}{AC}=\frac{1}{4}\\\frac{KN}{28}=\frac{1}{4}\\4\cdot KN=1\cdot 28\\KN=\frac{28}{4}=7
Ответ: 7.