Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B . Найдите диаметр окружности, если AB = 3, AC = 9.
Источник: statgrad
Решение:
Проводим отрезок ВО. Он будет являться радиусом окружности и перпендикуляром к касательной АВ:
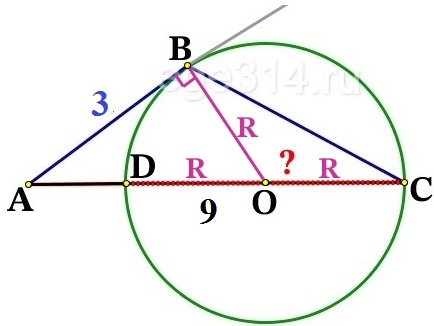
В полученном прямоугольном ΔАВО АВ = 3, ВО = R, АО = АС – R = 9 – R. По теореме Пифагора найдём R:
АO2 = AB2 + BO2
(9 – R)2 = 32 + R2
81 – 18R + R2 = 9 + R2
–18R + R2 – R2 = 9 – 81
–18R = –72
R = –72/(–18) = 4
Найдём диаметр окружности, он равен двум радиусам:
d = 2R = 2·4 = 8
Ответ: 8.