Решение №3867 Постройте график функции y=(4,5|x|-1)/(|x|-4,5x^2).

Постройте график функции

$y=\frac{4,5|x|–1}{|x|–4,5x^{2}}$

Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.

Источник: statgrad

Решение:

ОДЗ: |x| – 4,5x² ≠ 0
при х ≥ 0:
+x – 4,5x² ≠ 0
x·(1 – 4,5x) ≠ 0
x ≠ 0
или
1 – 4,5x ≠ 0
–4,5x ≠ –1
x ≠ –1/(–4,5)
х ≠ $\frac{10}{45}=\frac{2}{9}$
при х < 0:
–x – 4,5x² ≠ 0
x·(–1 – 4,5x) ≠ 0
x ≠ 0
или
–1 – 4,5x ≠ 0
–4,5x ≠ 1
x ≠ 1/(–4,5)
х ≠ $–\frac{10}{45}=–\frac{2}{9}$

Раскрываем модуль:

$\begin{cases} \frac{4,5(+x)–1}{(+x)–4,5x^{2}} =\frac{4,5x–1}{–x\cdot (–1+4,5x)}=\frac{1}{–x}=–\frac{1}{x}\color{Blue} ,x>0\\ \frac{4,5(–x)–1}{(–x)–4,5x^{2}} =\frac{–4,5x–1}{x\cdot (–1–4,5x)}=\frac{1}{x}\color{Blue} ,x<0\end{cases}$

Найдём координаты точек не принадлежащих графику:

$y(\frac{2}{9})=-\frac{1}{\frac{2}{9}}=–4,5\\y(–\frac{2}{9})=\frac{1}{–\frac{2}{9}}=–4,5$

( $\frac{2}{9}$ ; –4,5) ∉ графику функции
(– $\frac{2}{9}$ ; –4,5) ∉ графику функции

y = $\color{Magenta} -\frac{1}{x}$ , x > 0, гипербола

x	0,5	1	2
y	–2	–1	–0,5

y = $\color{DarkGreen} \frac{1}{x}$ , x < 0, гипербола

x	–0,5	–1	–2
y	–2	–1	–0,5

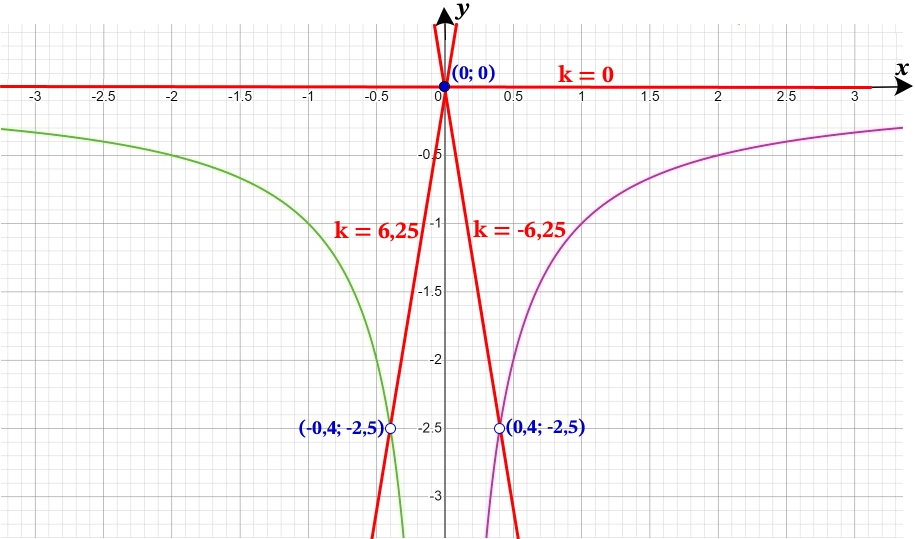
y = kx, прямая проходящая через начало координат (0; 0).
1) y = 0·x
k = 0
2) Проходит через точку ( $\frac{2}{9}$ ; –4,5):
–4,5 = k· $\frac{2}{9}$
k = –4,5/ $\frac{2}{9}$ = –20,25
3) Проходит через точку (– $\frac{2}{9}$ ; –4,5):
–4,5 = k·(– $\frac{2}{9}$ )
k = –4,5/(– $\frac{2}{9}$ ) = 20,25

Ответ: –20,25; 0; 20,25.