Решение №4184 На координатной плоскости изображены векторы a→ и b→. Найдите длину вектора 2a→

На координатной плоскости изображены векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ . Найдите длину вектора 2 $\overrightarrow{a}$ − $\overrightarrow{b}$ .

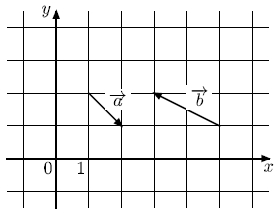
Источник: statgrad

Решение:

$2\overrightarrow{a}-\overrightarrow{b}=2\cdot \overrightarrow{a}+(-\overrightarrow{b})$

Вектор а увеличим по длине в 2 раза, у вектора b поменяем направление на противоположное, сохранив угол наклона и перенесём его начало в конец вектора а:

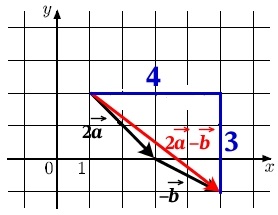
Искомое длину вектора 2 $\overrightarrow{a}$ − $\overrightarrow{b}$ , можно найти как гипотенузу прямоугольного треугольника по теореме Пифагора:

x² = 4² + 3²
х² = 16 + 9
х² = 25
х = √25 = 5

Ответ: 5.