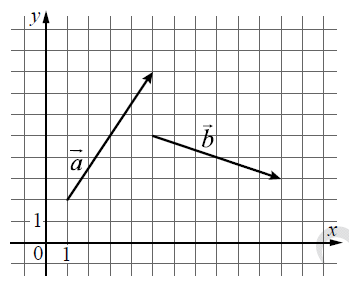
На координатной плоскости изображены векторы \overrightarrow{a} и \overrightarrow{b}. Найдите скалярное произведение \overrightarrow{a}\cdot \overrightarrow{b}.
Источник: fipi
Решение:
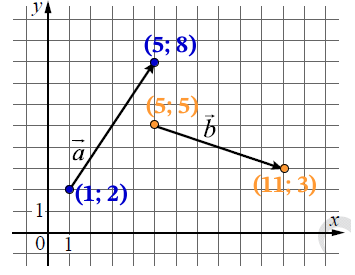
Найдём координаты векторов, найдя на рисунке координаты точек начала и точек конца каждого вектора:
\overrightarrow{a}\left\{x_{2} -x_{1};y_{2}-y_{1} \right\}=\overrightarrow{a}\left\{5 -1;8-2 \right\}=\overrightarrow{a}\left\{4;6\right\} \\ \overrightarrow{b}\left\{x_{2} -x_{1};y_{2}-y_{1} \right\}=\overrightarrow{b}\left\{11 -5;3-5 \right\}=\overrightarrow{b}\left\{6;-2\right\}
Найдём скалярное произведение векторов:
\overrightarrow{a}\cdot \overrightarrow{b}=x_{1}\cdot x_{2}+y_{1}\cdot y_{2}=4\cdot 6+6\cdot (-2)=24-12=12
Ответ: 12.